Merge Sort

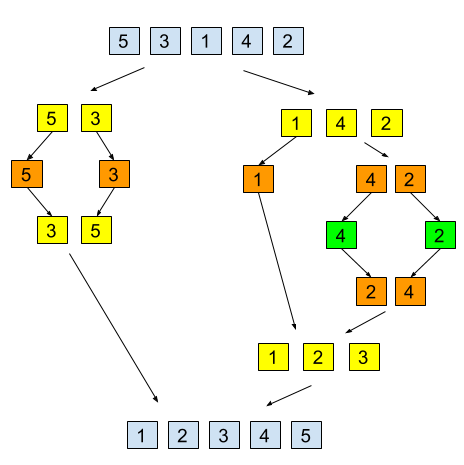
Recursion diagram of an array being
sorted via merge sort.

My partner and I were tasked to do a presentation on merge sort for the AP ICS course. Merge sort is one of the more complex sorting algorithms, but that complexity comes with the advantage that merge sort is one of the fastest sorting algorithms. Many merge sort implementations (including ours) are recursive, although it is possible to do merge sort iteratively. In general most merge sort algorithms come in two major sections, splitting, and merging.

Splitting

The first part of the algorithms is splitting. A copy of the bottom half of the array is created, and a copy of the top half of the array is created. Then merge sort is called on each of those arrays. This continues until the length of the array is 1, which is the base case. Consider the following code for splitting the array:

int[] lowerTarget = Arrays.copyOfRange(target, 0, target.length / 2);
int[] upperTarget = Arrays.copyOfRange(target, target.length / 2, target.length);
lowerTarget = sortInt(lowerTarget);
upperTarget = sortInt(upperTarget);