Merge Sort
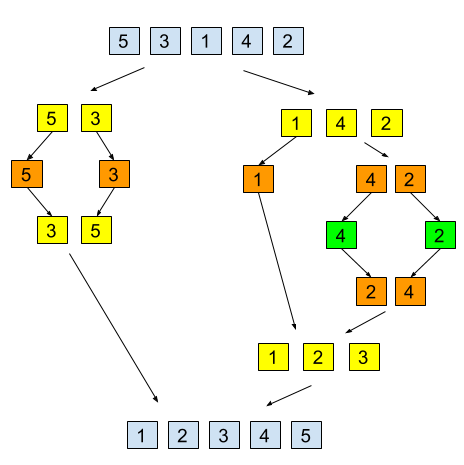
Recursion diagram of an array being
sorted via merge sort.
My partner and I were tasked to do a presentation on merge sort for the AP ICS course. Merge sort is one of the more complex sorting algorithms, but that complexity comes with the advantage that merge sort is one of the fastest sorting algorithms. Many merge sort implementations (including ours) are recursive, although it is possible to do merge sort iteratively. In general most merge sort algorithms come in two major sections, splitting, and merging.
Splitting
The first part of the algorithms is splitting. A copy of the bottom half of the array is created, and a copy of the top half of the array is created. Then merge sort is called on each of those arrays. This continues until the length of the array is 1, which is the base case. Consider the following code for splitting the array:
int[] lowerTarget = Arrays.copyOfRange(target, 0, target.length / 2);
int[] upperTarget = Arrays.copyOfRange(target, target.length / 2, target.length);
lowerTarget = sortInt(lowerTarget);
upperTarget = sortInt(upperTarget);
This code means that the longer the array, the more copies of it need to be stored. The number of copies of the array is proportional to the logarithm of the length of the array since it keeps on being divided in two. In the above image each different colour represents the depth of recursion, and thus also the number of copies of the array.
Merging
The second party of merge sort is the merging of the two arrays. Since we know that the two arrays will be sorted due to the base case, we only need to look at the first non added element in each array. Consider the following source code:
int[] endArray = new int[target.length];
int endArrayPointer = 0, lowerTargetPointer = 0, upperTargetPointer = 0;
while (endArrayPointer < endArray.length)
if (lowerTargetPointer == lowerTarget.length)
endArray[endArrayPointer++] = upperTarget[upperTargetPointer++];
else if (upperTargetPointer == upperTarget.length)
endArray[endArrayPointer++] = lowerTarget[lowerTargetPointer++];
else if (lowerTarget[lowerTargetPointer] < upperTarget[upperTargetPointer])
endArray[endArrayPointer++] = lowerTarget[lowerTargetPointer++];
else
endArray[endArrayPointer++] = upperTarget[upperTargetPointer++];
The code will loop until the entire sorted array is filled up. The first twos if statements handle the cases where either the lower or upper arrays have been exhausted into the sorted array. The next two cases simply compare the first non added value from each array, and add the smaller one to the sorted array.
Efficiency
As previously mentioned the number of copies of the array is proportional to the length of the array, and each of these copies need to be reassembled. Since we know assembly is done in linear time, therefore the time completely of merge sort is O(N*log(N)) where N is the length of the array. Compared to other sorting algorithms such as bubble sort, merge sort runs at break-kneck speeds. The fact that there are multiple copies of the array make the algorithm less memory efficient, however the logarithm grows incredibly slowly, and due to Java’s current limitations, the largest possible array will only need to be copied 31 times.
Example
| Example Files |
|---|
| Array.data |
| Main.java |
| Merge.java |
For the presentation my partner and I needed to implement a working merge sort. To demonstrate its speed we decided to have the program read in one million integers and sort them. On my machine this takes less than a second, however this may vary due to computer and storage device speed.
This project solidified the concept of efficiency and time completely as merge sort takes an incredible amount of time to sort the same array. This assignment made me consider time complexity more when making projects.